EMPOWERMENT IN MATHEMATICS EDUCATION
Paul Ernest
University of Exeter, United Kingdom
In this paper I explore the meaning of empowerment in the teaching and learning of mathematics. The main part of the paper is devoted to distinguishing three different but complementary meanings of empowerment concerning mathematics: mathematical, social and epistemological empowerment. Mathematical empowerment concerns gaining the power to use mathematical knowledge and skills in school mathematics. Social empowerment is the ability to use mathematics for social betterment. Epistemological empowerment means confidence and personal power over the use, creation and validation of knowledge. After analysing what these three interpretations of empowerment mean, I relate them to the theme of equity.
What is empowerment?
Empowerment is the gaining of power in particular domains of activity by individuals or groups and the processes of giving power to them, or processes that foster and facilitate their taking of power. Thus a discussion of mathematical empowerment concerns the aims of teaching mathematics and the objectives of learning mathematics. It also concerns the role of mathematics in the life of the individual learner and its impact on their school and wider social life, both in the present and in the future. Empowerment through mathematics necessitates a consideration of the development of the identity of learners and their potentiation through the development mathematical and related capacities.
Conceptually, it is useful to distinguish three different domains of empowerment concerning mathematics and its uses, although these are neither wholly discrete nor unrelated in their modes of functioning. These three domains of empowerment may be described as mathematical, social, and epistemological.see note 1
Mathematical empowerment concerns the gaining of power over the language, skills and practices of using and applying mathematics. This is the gaining of power over a relatively narrow domain e.g. that of school mathematics.
Social empowerment through mathematics concerns the ability to use mathematics to better one's life chances in study and work and to participate more fully in society through critical mathematical citizenship. Thus it involves the gaining of power over a broader social domain, including the worlds of work, life and social affairs.
Epistemological empowerment concerns the individual's growth of confidence not only in using mathematics, but also a personal sense of power over the creation and validation of knowledge. This is a personal form of empowerment: the development of personal identity so as to become a more personally empowered person with growth of confidence and potentially enhanced empowerment in both the mathematical and social senses (and for the mathematics teacher - enhanced professional empowerment).
Mathematical empowerment
Mathematical empowerment may be viewed from two complementary perspectives, the cognitive and the semiotic. The former is the more familiar and traditional psychological perspective in terms of mental 'objects' and activities (English and Halford 1995, Lesh and Landau 1983), whereas the latter is a more social / cultural perspective focussing on activity and actions with symbols and texts within social contexts (Lerman 1994).
From a cognitive psychology perspective, mathematical empowerment concerns the 'acquisition' of the facts, skills, concepts and conceptual structures of mathematics, and the general strategies of problem solving (Bell et al. 1983). Thus from this perspective, the successfully empowered learner should demonstrate an appropriate range of mathematical capabilities such as performing algorithms and procedures, computing solutions to exercises, solving problems, and so on. Clearly such cognitive capabilities are an important outcome of learning of mathematics. They include using and applying facts, skills, concepts and all forms of mathematical knowledge. They also include applying general and topic specific mathematical strategies, and carrying out plans and approaches in solving mathematical problems. Lastly they include the posing of mathematical problems and the ability to judge the correctness of proposed solutions.
More recently some researchers have emphasised the need for meta-cognitive skills too. Metacognitive activities involve planning, monitoring progress, making effort calculations (e.g. "Is this approach too hard or too slow?"), decision making, checking work, choosing strategies, and so on. Metacognition (literally: above or beyond 'cognition') is about the management of thinking.
According to Flavell (1976: 232)
'Metacognition' refers to one's knowledge concerning one's own cognitive processes and products and anything related to them. … metacognition refers, among other things, to the active monitoring and consequent regulation and orchestration of these processes in relation to the cognitive objects or data on which they bear, usually in the service of some concrete goal or objective.
Evidently metacognitive capabilities are an important part of mathematical empowerment. They also represent some of the 'cognitive' elements of epistemological empowerment discussed below.
From a semiotic perspective, mathematical empowerment consists of the development of power over the signs of mathematics, that is the 'texts' of mathematics within their social context. Here the word 'text' is used in its broadest semiotic sense to mean any simple or elaborate constellation of signs, be they symbols, indices, icons (Peirce 1931-58) or a mixture, together with the social nexus of their use (Ernest 1993, 1998a). The semiotic perspective of mathematical activity is less well developed than cognitive perspectives (including constructivism), but some of the features are as follows.
Semiotic capabilities in mathematics include the following.
The first two abilities are more traditionally glossed in terms of understanding and solving mathematical problems, both routine and non-routine. The third corresponds to mathematical problem posing or task setting. The fourth ability comprises evaluation capabilities in reading and judging the correctness of mathematical solutions. Overall, from this semiotic perspective mathematical empowerment comprises the ability to make sense of, write and judge the correctness of mathematical texts concerning mathematical tasks and questions as well as their solutions and answers, including asking the questions themselves. Only when a person has mastered the four capabilities can they be said to be fully empowered mathematically, even if the domain of application of these abilities is limited (e.g., to a significant part of school mathematics).
I have contrasted the cognitive and semiotic perspectives because of the different interpretations of mathematical mastery that they provide. From a cognitive perspectives the focus is on what goes on in the mind of the individual, with external behaviours as secondary manifestations. From a semiotic perspective the external representations and texts and their social functions and meanings come first, with the individual learner's sense-making, interpretations and symbolic responses acquired from and developed through participation in the social and cultural context in which texts and tasks are always embedded. The difference between these two perspectives hinges on the synchronic focus of the cognitive on the learner acquisition of schemas or cognitive structures versus the diachronic focus of the semiotic perspective on what is primarily external or socially displayed semiotic activity in writing texts over time. This potentially offers an enriched view of mathematical activity, although at present it must be conceded that this is a far less developed and hence less enlightening perspective than that of the cognitive.
In summary, from either perspective mathematical empowerment consists of power over the language, symbols, knowledge and skills of mathematics and the ability to confidently apply this in mathematical applications within the context of schooling, and possibly to a lesser extent, outside of this context.
Social empowerment
There is a continuum of ways in which mathematics can contribute to social empowerment from the straightforwardly utilitarian to the more politically radical 'critical mathematical citizenship'. In the minimal utilitarian way, success at mathematics gives students power through enhanced life chances in study, the world of work, and social affairs. Thus developing applicable capabilities in mathematics often benefits the student directly in these domains. However, quite often it is personal certification in the form of examination and test results and certificates that serve as evidence of the student's capabilities which open the doors of social opportunity. Typically such formalised achievement documentation is required by 'gatekeepers' for admittance to advanced study and also to many rewarding occupations.
Although certification requirements extend beyond this one subject, qualifications in mathematics are accorded a privileged role and have unique social significance via these 'gatekeepers'. The use of mathematical qualifications as a 'critical filter' controlling entry into higher education and higher paid occupations has long been noted, especially by researchers in the area of gender and mathematics (e.g., Sells 1973, 1976, Walkerdine 1997). Although this is particularly notable in occupations involving scientific and technological skills, it extends far beyond this domain to many other occupations, including education, the caring professions, financial services and management positions in business and commerce. This has important implications for social equity, especially in the area of gender and mathematics. For in many anglophone western countries there are widespread patterns of girls' and women's lower participation rates in advanced mathematics study, as well as lower examination attainments during schooling. The latter may be diminishing but the overall 'critical filter' effect, in combination with other social factors, still results in many women getting lower paid work, thus sustaining and reproducing gender inequity in society (Ernest 1995). Similarly, differential patterns of mathematical and general educational achievement by social class, long noted by researchers (e.g., Task Group on Assessment and Testing 1988) also has important implications for social equity.
At the other end of the social empowerment continuum is critical mathematical citizenship. This involves the development of mathematically-literate or socially-numerate citizens who are able to exercise independent critical judgements with regard to the mathematical underpinnings of crucial social and political decision-making, as well as the uses of mathematics in the mass-media, advertising, and in commercial, political and interest group pronouncements and propaganda. The idea of 'being critical' involved here is not the same as the popular meaning of being inclined to judge severely and find fault, calling attention to petty errors and flaws. Instead 'being critical' is about engaging in a critique; it means making careful judgements, using all available evidence, reasoning and balanced arguments to evaluate claims and to reach conclusions. It also means not taking explanations and views of tradition or 'authorities' for granted but questioning them to see if they stand up to careful and challenging scrutiny. Above all it means independent thinking, which draws upon the larger contexts and implications of the issue under consideration, as well as detailed knowledge, to make balanced judgements.
There is a tradition of critical mathematics education that is about this critical attitude of mind applied to mathematics and its teaching (Ernest 1991, Skovsmose 1994), and there are two main sets of questions underpinning it. The first set of questions is about the nature of mathematics itself. Is it the superhuman realm of timeless certainty consisting only of objective and value-free knowledge? Or are there other ways of conceptualising mathematics in more human, cultural and historical ways? These questions also have relevance for the third form of empowerment discussed below: epistemological empowerment.
The second set of questions that a critical perspective poses, concerns the aims and purposes of teaching and learning mathematics. What are and what should be the aims of teaching and learning mathematics? Whose aims are these? For whom are they intended? Based on whose values? Does mathematics education operate so as to favour some groups at the expense of others? If so just who gains and who loses in this process? How should mathematics learning empower learners in their lives and in relation to society? What can a critical mathematics education do for learners? Can it provide a critical mathematical literacy strengthening citizenship and furthering justice for all in modern society, or does it simply create more canny consumers?
According to the critical mathematics education perspective students should be able to think mathematically, and be able to use their mathematical knowledge and skills in their lives to empower themselves both personally and as citizens, and through their broadened perspectives, to appreciate the role of mathematics in history, culture, and the contemporary world.
A critical mathematics education would hope to develop some of the following aspects of understanding and awareness:
In short, critical mathematics education should give learners an appreciation and awareness of the nature and value of mathematics and the uses to which it is put, as well as understanding and being able to critique its social uses.
However, this is not supposed to be a list of yet more content that is to be added to what is already present in the standard curriculum. The key issue is that if this emphasis is intended to empower learners, these need to be live aspects of awareness. They need to link to the real interests, enthusiasms and experiences of students. All students bring with them an extensive range of knowledge and experience from everyday life, the world of work and the social and cultural milieu in which they live. These include their knowledge and involvement in local affairs, leisure activities, pastimes, hobbies, clubs, and the media including popular music, video games, television, films, magazines and newspapers. There is an extensive range of issues involved, including local, national and global politics, environmental issues, health, fitness, sport, nutrition, drugs, education, policing, law and order, finance, housing, transport, accidents and safety, and so on. This list indicates the breadth of the domains across which socially and mathematically empowered students and others should be to apply their critical mathematical-literacy skills. It also indicates the richness of the range of issues, shared to a greater or lesser extent by students, and threading through their lives, which can be drawn upon as meaningful resources for contextualising the teaching and learning of mathematics in seeking to socially empower them through mathematics. Authentic materials, social statistics, and other resources thus provide a basis for understanding how mathematics is used and applied in the world outside school. In particular, they can be used to teach students to identify, interpret, evaluate and critique the mathematics embedded in social, commercial and political claims, and the uses made of them in advertisements and claims in the mass media to those of political parties as well as government claims.
In the development of critical mathematical literacy and citizenship through the appropriate use of authentic materials and a critical pedagogy, independent critical judgement is developed in the student, in a way that should be individually empowering. The empowered learner will not only be able to pose and solve mathematical questions (mathematical empowerment), but also will be able to understand and begin to answer important questions relating to a broad range of social uses and abuses of mathematics (social empowerment). Many of the issues involved will not seem primarily to be about mathematics, just as keeping up to date about current affairs from reading broadsheet newspapers is not primarily about literacy. Once mathematics becomes a 'thinking tool' for viewing the world critically, it will be contributing to both the political and social empowerment of the learner, and hopefully to the promotion of social justice and a better life for all.
Recent developments in citizenship in the British National Curriculum (DFEE and QCA, 1999) provide encouragement for including such approaches in secondary schools. For pupils aged 14 to 16 years of age this new curriculum development includes the following two objectives (reformulated here) as legal requirements.
These new requirements include many of the factors, when applied to mathematics, that make up the critical mathematical literacy aspect of social empowerment as defined above. However the authors of these requirements probably did not have mathematics specifically in mind as the intended vehicle for these aspects of education, except in the very limited domain of social statistics. This raises the question: Do pupils really need to be able to see the world through mathematical eyes to be effective citizens in modern society, when most of these concerns are general and not mathematical?
From a critical mathematics education perspective they do, because the mathematisation of modern society and modern life has been growing exponentially. Today, virtually all human activities and institutions are conceptualised, regulated and communicated numerically, including sport, popular media, health, education, government, politics, business, commercial production, and science. For example, sports records are numerical, as are music charts and those for best selling books.
Many aspects of modern society are controlled by complex hidden mathematical systems, such as supermarket checkout tills with automated bill production and stock control; tax systems; welfare benefit systems; industrial, agricultural and educational subsidy systems; voting systems; stock market systems. These automated systems carry out complex tasks of information capture, policy implementation and resource allocation. The point is that complex mathematics is used to regulate many aspects of our lives, e.g., our finances, banking and bank accounts, with very little human scrutiny and intervention once the systems are in place. Only through a critical mathematics education can future citizens learn to analyse, question and challenge these systems that can distort life chances and reduce freedoms.
Already, we view our lives and the world about us through a highly quantified framework. Our understanding is framed by the clock, calendar, work timetables, travel planning and timetables, finances and currencies, insurance, pensions, tax, measurements of weight, length, area and volume, graphical and geometric representations, etc. Much of our experience of life is already mathematised. Unless schooling helps learners to develop the knowledge and understanding to identify these mathematisations of our world, and the confidence to question and critique them, they cannot be in full control of their own lives, nor can they become properly informed and participating citizens. Consequently, they may be manipulated by commercial, political or religious interest groups, or may become cynical and irrational in their attitudes to social, political, medical and scientific issues.
The mathematisation of modern society and is more than a neutral language that serves as a useful tool. It also embodies a set of values about what is socially possible and desirable. Thus economics as used in modern society is not merely a neutral description of the flow of resources. It also represents a perspective that maintains the status quo, dehumanising discussions of military expenditure, social welfare, world debt, etc. It is not easily possible to question the pronouncements of political and commercial authorities in such areas of policy unless one has the skills and confidence to understand and sometimes challenge the applications of mathematics, and the hidden assumptions upon which they rest.
The goal of critical mathematical education is the empowerment of learners both as individuals and as citizens-in-society. This is achieved by developing mathematical power both to overcome barriers to higher education and employment and thereby to increase economic self-determination; and to foster critical awareness and democratic citizenship via mathematics. Ultimately, the long-term aim is social change via the empowerment of the citizenry towards a more just and egalitarian society. In other words, the aim is to strengthen democracy, not to overthrow it.
What does critical mathematics education mean in terms of classroom practice? The aims of critical mathematics, require the use of a questioning and decision making learning style in the classroom. Teaching approaches should include discussions, permitted conflict of opinions and views but with justifications offered, the challenging of the teacher as an ultimate source of knowledge (not in their role as classroom authority), the questioning of content and the negotiation of shared goals. Some of this is included in the new Citizenship requirements in the National Curriculum. Also the learners should be given the chance pose their own problems and initiate their own projects and investigations at least some of the time, as did the children of the School of Barbiana (1970). Learning materials should include socially relevant projects, authentic social statistics, should accommodate social and cultural diversity, and use local cultural resources. However the approach must also honestly and openly address the instrumental and life goals of the learners themselves, both in terms of needed skills and passing exams.
However, using mathematics for political and social understanding and empowerment has always been controversial. A counter-argument against such an approach is that it can become propaganda and a political misdirection of the young in itself. But, as anyone who has taught contentious issues in the mathematics classroom or lecture hall in a democratic country knows, such an approach invariably results in dispute and heated argument rather than in passive acceptance. The pupils of today will not accept teacher propaganda without question. The safeguard built into the critical mathematics education approach is that it encourages students to think for themselves and to apply their skills in independent appraisals of contentious issues based on balanced reasoning and arguments constructed by themselves. As long as this independence remains at the heart of critical mathematics education, then it cannot degenerate into polemics and political propaganda.
Examples of critical mathematics education approaches are embodied in Marilyn Frankenstein's numeracy course for adults (Frankenstein, 1989), and the Radical Statistics Group's publications (for example, Irvine, Miles and Evans, 1979). In schools, developments in anti-racist and anti-sexist mathematics perhaps have gone the furthest in this direction. A discussion of the underlying philosophy of critical mathematics education as well as accounts of project work with secondary school children in Scandinavia can be found in the work of Steig Mellin-Olsen (1987) and Ole Skovsmose (1994). See also Abraham and Bibby (1988) and Ernest (1991).
A successful critical mathematics education must succeed in empowering the learner, first to overcome internal inhibitions and perceptions of inadequacy, second to question the teacher, the subject and the constraints of school, and third to question the 'facts' and edicts of authority at large in society. In a word, to become socially empowered through mathematics. However, past experiences often give learners an unquestioning acceptance of authority in school, society and mathematics. This may be manifested in lack of confidence, in passivity or even in aggression. Students including adult returners to education cannot become autonomous learners and confident critical citizens immediately. They also need to be epistemologically empowered, i.e., to benefit from the third sense of empowerment distinguished above.
Epistemological empowerment
This third sense concerns the individual's growth of confidence not only in using mathematics, but also a personal sense of power over the creation and validation of knowledge. This is a personal form of empowerment: the development of personal identity so as to become a more personally empowered person with growth of confidence and potentially enhanced empowerment in both the mathematical and social senses (and for the mathematics teacher - enhanced professional empowerment - see note 1).
Many students and other individuals, including mathematics teachers (Cooper, 1989), are persuaded by the prevailing ideology that the source of knowledge is outside themselves, and that it both created and sanctioned solely by external authorities. They are led to believe that only such authorities are legitimate epistemological agents, and that their own role as individuals is merely to receive knowledge, with the subsequent aim of reproducing or transmitting it as accurately as possible. Thus despite being knowers (that is 's/he who knows'), most individuals are disempowered as epistemological agents.
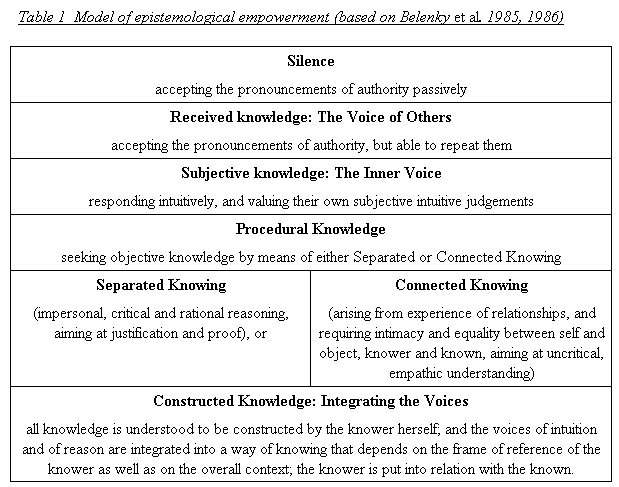
In order to explore this dimension of empowerment, of the three considered here perhaps the most neglected in discussions of the aims of teaching and learning of mathematics, it is valuable to turn to models of the development of the individual knower. There are a number of such models, but that of Belenky et al (1986) is the most relevant in the present context because of its direct focus on the developing epistemological powers of the individual.(see note2) Belenky et al. (1986) provide a valuable model of the stages of empowerment of the knower, in which students develop as epistemological agents from a position of complete passivity (passive receivers of knowledge) dominated by authority to one of epistemological autonomy and empowerment, as they progress through the stages shown below (Table 1).
This model, known as Women's Ways of Knowing, and was originally developed as part of a feminist research project to describe the progress of adult women knowers. It was also developed as a corrective to what was perceived to be the male bias in the theory of William Perry (1970) concerning intellectual and ethical development (primarily of males) during the college years. It incorporated Carol Gilligan's (1982) distinction between separated and connected styles of ethical reasoning which correlates separated values and thinking with stereotypical masculinity and connected values and thinking with stereotypical femininity.(see note3)
Like a number of other researchers I assume that the application of the model to school-age students of either sex and is legitimate. For example, Becker (1996) interviewed a number (31) of students of mathematics of both sexes, and interpreted their personal views of mathematics and knowledge using the Belenky et al. model. While she found a good match for their views of knowing, few were at the final 'constructed knowing' stage, and overall they did not fit neatly into gender categories, with both male 'connected knowers' and female 'separate knowers'. She found the model useful, but expressed concern that she was fitting the data into a pre-existing framework, rather than letting a theory emerge from the data, in the 'grounded theory' approach (Glaser and Strauss 1968).
The model shown in Table 1 offers a hierarchy of stages of epistemological empowerment, from the passive, silent reception of knowledge from authority, through to the active construction of knowledge coupled with awareness of this power. Thus the strength of this theory is that it accounts for the range of relative positions, including power relationships, that hold between knowledge users and knowledge creators or authorities. One, the subject, is the receiver and user of knowledge (explicitly treated in the theory). The 'other', implicit in the account, is the external source of knowledge and authority.
The range of relationships begins with the complete domination of the subject by the 'other' in authority, in the stages of Silence and Received Knowledge. In these cases the transmission metaphor in its most authoritarian form reigns supreme, with the subject being the passive recipient of the absolute knowledge from the 'other'. This case describes the position of many learners of mathematics, who accept that they must simply receive knowledge unquestioningly from the teacher, and who believe that there are no other touchstones for its validity. In the first stage the learner or subject has no agency or power and simply receives passively. In the second stage, the learner has the power to 'parrot' the received knowledge, that is, to utter the same pronouncements simply and solely on the authority of the teacher.
In the stage of Subjective Knowledge, the transmission metaphor still dominates, but the subject may passively resist the knowledge and authority of the 'other', preferring to listen to her own intuition or 'gut feeling'. This describes how many learners in mathematics prefer their own informal methods which they intuitively feel to be safer to new ones provided by the teacher which the learner does not yet feel she 'owns' (Hart, 1981).
At the stage of Procedural Knowledge, the subject is no longer overpowered by the 'other' as an unquestioned epistemological authority. The subject is able to seek and justify objective knowledge by means of either the Separate or the Connected Knowing approaches.
Separate Knowing is a new, rational mode in which the subject realises that there are objective logical criteria and rules for justifying and criticising knowledge, and uses them. Authority supplies these criteria as unquestioned assumptions and rules out as irrelevant matters that do not fall within their sphere. However, within the field of application of the rational criteria, all knowledge claims can be scrutinised for correctness, and criticised, and new knowledge claims can be put forward. In the learning of mathematics this form of knowing can encompass mastery of notation, symbolism and syntax. Also an emphasis on following procedures, logical reasoning, proof and correctness.
Connected Knowing is an elaboration of the intuitive knowing of the previous stage, and arises from an immersion in the domain of experience. This mode of knowing involves a rapprochement between the knower and known; an intimacy with the inner relationships of the area of knowledge which give them meaning and plausibility. In the learning of mathematics, this can involve the understanding of conceptual links, and the use of reasoning processes and general strategies to conjecture mathematical relationships. To a partial extent this matches Skemp's (1976) idea of 'relational understanding'.
At the stage of Constructed Knowing, the subject is an autonomous epistemological agent, and does not make concessions to the 'other' in authority. The subject has the confidence to integrate both connected and separate knowing, and to question the foundations and assumptions implicit in any inquiry, as well as to pose new questions. In the learning of mathematics, the constructed knower questions new items of knowledge, and relates them to the body of mathematical knowledge and to human purposes and culture. She also able to pose new mathematical problems, and explores approaches to them, and shares the outcome with peers and teachers.
If we apply this model to school children, most of them will best be described as being in the early stages. They may have acquired some of the knowledge and means of doing mathematics at school but because of the 'disconnected' way in which mathematics is usually taught it will probably just be a small compartment in their lives and a way of thinking that they bring out in the mathematics classroom. If they succeed in mathematics hopefully they develop the ability to apply some of the features of the intermediate stages, but this may still leave mathematics as something technical and little to do with their lives and experiences. Very few will be able to relate to mathematics through connecting different areas of their own knowledge. This is primarily about intuition and an 'inside knowledge' of mathematical concepts. (Feeling you can get inside mathematical ideas, and feeling that they have some life inside your imagination too.) The ultimate goal, according to this model, is to achieve the stage of being a 'constructing knower', where you can combine intuition and the procedures and skills of mathematics to make sense of the world and confidently apply mathematical thinking to it.
What this model suggests is that to achieve the epistemological empowerment of learners through mathematics it is not enough for them to gain mastery over some mathematical knowledge and skills. There needs to be a personal engagement with mathematics so that it becomes an integral part of the learner's personal identity. This means that the learners need to:
These are very ambitious goals for school mathematics. Such goals can very likely only be achieved over the long term. Probably the most important factor will be the quality of student-teacher relationships in the mathematics classroom. In case studies where learners have suddenly surged ahead and been mathematically empowered the catalyst has usually been personal encouragement by the teacher and the establishment of a personal relationship with the teacher after some success in a special student project (e.g., Womack 1983).(see note4)
A number of factors seem to be important:
Based on both a theoretical analysis and on professional experience, these appear to be the most important factors. However, even if these recommendations were based on research evidence there would be no guarantees that implemented over an extended period of time they would succeed in empowering all learners as epistemological agents. Human beings are complex and self-constructing entities and their reactions are simply not mechanistically predictable. In some cases not all factors will be necessary. Indeed, as indicated above, sometimes a single incident can initiate a shift towards engagement, confidence and epistemological empowerment. In other cases, despite the best efforts of teachers to structure classroom mathematics in these listed ways students may not gain the required confidence or sense of autonomy. After all, experiences in mathematics classes contribute only a small part to learner identity construction. Other factors such as emotional insecurity or strong peer identification may overwhelm such positive experiences. Nevertheless over an extended period these factors should have a dramatic impact on the confidence and mathematical powers of most students.
Of course the social context of teaching and the constraints and opportunities it provides will limit the opportunity of many teachers to teach mathematics in these ways. Indeed teachers themselves need to be professionally empowered as near-autonomous agents to have the confidence to work in such ways.
Conclusion: Empowerment and Equity
The aim of empowering learners as epistemological agents is a radical and summative one, as it brings together and integrates all three of the different types of empowerment discussed above. First, there is the need for learners to master some significant sub-domain of school mathematics confidently (mathematical empowerment). Second, there is the need to be socially empowered through mathematics, both through increasing study and employment opportunities via applicable skills and examination successes, and through the powers of 'critical mathematical citizenship'. Third, the epistemological empowerment of learners also involves their development of personal confidence, their sense of mathematical self-efficacy, as well as their sense of personal ownership of and power over mathematics. Only when all of these powers are developed will they feel they are entitled to be confident in applying mathematical reasoning, judging the correctness of such applications themselves, and critically appreciating (including rejecting, in some cases) the applications and uses of mathematics by others, across all types of contexts, in school and society. Thus epistemological empowerment is the culmination of the other types of empowerment discussed here.
What are the implications for equity through mathematics? Implicit in my analysis is the assumption that enabling learners to become mathematically empowered will enhance their capabilities and confidence in all forms of using and applying mathematics, and hence their levels of attainment in mathematics by whatever means they are measured. On this assumption, the first step towards equity is to provide equal opportunities for all learners to become empowered mathematically. This means implementing long-term programmes through which learners develop the mathematical capabilities, the skills of using and applying mathematics, and confidence and a sense of personal ownership of mathematics. Much is already known about achieving these goals, although these proposals suggest an increased emphasis on social and epistemological empowerment in mathematics.
A legitimate criticism is that my discussion of empowerment is primarily individualistic, for I have mainly looked at the powers that can be developed by individuals, with little attention to their membership within societal groups and with no attention to the relationships between sectors. But there are well known structural and systemic differences which favour some groups and inhibit the progress of others. Although this is irrefutable, an empowerment perspective can nevertheless address some of the problems of inequity. For example, one of the enduring patterns of mathematical difference in terms of gender in Anglophone Western countries is the lower mean measures of confidence and self-efficacy (especially in terms of Attribution Theory) of girls and women (see, e.g., Ernest 1998b). This can be read in terms of differential levels of epistemological empowerment by girls and women, since this encompasses confidence and self-perceptions of efficacy and autonomy.
References
Abraham, J. and Bibby, N. (1988) Mathematics and Society: Ethnomathematics
and the Public Educator Curriculum, For the Learning of Mathematics, 8 (2) 2-11.
Baxter Magolda, M. B. (1992) Knowing and Reasoning in College: Gender Related
Patterns in Student's Intellectual Development, San Francisco: Jossey Bass.
Becker, J. R. (1996) Research on gender and mathematics: One feminist perspective,
Focus on Learning Problems in Mathematics 18 (1, 2 & 3) 19-25.
Belenky, M. F., Clinchy, B. M., Goldberger, N. R. and Tarule, J. M. (1985) Epistemological
Development and the Politics of Talk in Family Life, Journal of Education, 167
(3) 9-27.
Belenky, M. F., Clinchy, B. M., Goldberger, N. R. and Tarule, J. M. (1986) Women's
Ways of Knowing, New York: Basic Books.
Bell, A. W., Küchemann, D. and Costello, J. (1983) A Review of Research
in Mathematical Education: Part A, Teaching and Learning, NFER-Nelson, Windsor.
Cooper, T. (1989) Negative Power, Hegemony and the Primary Mathematics Classroom:
A Summary, in Keitel, C. et al., Eds., Mathematics Education and Society (1989),
Paris: UNESCO, 150-154.
DFEE and QCA (1999) The National Curriculum for England: Citizenship, London:
Her Majesty's Stationery Office.
English, L. D. and Halford, G. S. (1995) Mathematics Education: Models and Processes.
Mahwah, New Jersey: Lawrence Erlbaum Associates.
Ernest, P. (1991) The Philosophy of Mathematics Education, London: Falmer Press.
Ernest, P. (1993) Mathematical Activity and Rhetoric: Towards a Social Constructivist
Account, in Hirabayashi, I. et al., Eds, Proceedings of PME-17 Conference, Tsukuba,
Japan: University of Tsukuba, 2, 238-245.
Ernest, P. (1995) 'Values, Gender and Images of Mathematics: A Philosophical
Perspective' International Journal for Mathematical Education in Science and
Technology, 26 (3) 449-462.
Ernest, P. (1998a) Social Constructivism as a Philosophy of Mathematics, Albany,
New York: State University of New York Press.
Ernest, P. (1998b) 'Introduction: Changing Views of 'the Gender Problem' in
Mathematics', V. Walkerdine, Counting Girls Out, New Edition, London: Falmer
Press, 1-14.
Flavell, J. H. (1976) metacognitive aspects of problem solving, in Resnick,
L. B. Ed. (1976) The Nature of intelligence, Hillsdale, New Jersey: Lawrence
Erlbaum, 197-218.
Frankenstein, M. (1989) Relearning Mathematics: A Different Third R - Radical
Maths, London: Free Association Books
Gilligan, C. (1982), In a Different Voice, Cambridge, Massachusetts: Harvard
University Press.
Glaser, B. G. and Strauss, A. L. (1968) The Discovery of Grounded Theory, London:
Weidenfeld and Nicholson.
Hart, K. Ed. (1981) Children's Understanding of Mathematics: 11-16, London:
John Murray.
Irvine, J., Miles, I. and Evans, J., Eds, (1979) Demystifying Social Statistics,
London: Pluto Press.
Lerman, S. Ed. (1994) Cultural Perspectives on the Mathematics Classroom, Dordrecht,
The Netherlands: Kluwer.
Lesh, R. and Landau, M. (1983) Acquisition of Mathematics Concepts and Processes,
London: Academic Press.
Loevinger, J. (1976) Ego Development, San Francisco: Jossey Bass.
Mellin-Olsen, S. (1987) The Politics of Mathematics Education, Dordrecht: Reidel.
Peirce, C. S. (1931-58) Collected Papers (8 volumes), Cambridge, Massachusetts:
Harvard University Press.
Perry, W. G. (1970) Forms of Intellectual and Ethical Development in the College
Years: A Scheme, New York: Holt, Rinehart and Winston.
School of Barbiana (1970) Letter to a Teacher, Harmondsworth: Penguin Books.
Sells, L. (1973) 'High school mathematics as the critical filter in the job
market', Proceedings of the Conference on Minority Graduate Education, Berkeley:
University of California, 37-49.
Sells, L. (1976) 'The mathematics filter and the education of women and minorities',
paper presented at the Annual Meeting of American Association for the Advancement
of Science, Boston, February 1976.
Skemp, R. R. (1976) 'Relational Understanding and Instrumental Understanding',
Mathematics Teaching, 77, 20-26.
Skovsmose, O. (1994) Towards a Philosophy of Critical Mathematics Education.
Dordrecht: Kluwer.
Task Group On Assessment and Testing (1988) A Report, London: Department of
Education and Science.
Walkerdine, V. (1997) Counting Girls Out, London: Falmer Press.
Womack, D. (1983) 'Seeing the Light', Times Educational Supplement, 8 April
1983.
Footnotes